返回
顶部

https通信过程

前言

前段时间给自己的网站上了个https证书，因此想借此机会深入了解一下https通信的过程，借助wireshark和万能的搜索引擎，稍微进行了一些调查，总结出这篇文章

参考链接：

TLS中的key exchange（密钥交换）

以前我一直以为https交换密钥的过程就是客户端随机出来一个对称加密算法的密钥，然后使用证书的公钥加密发送给服务器，服务器使用自己的密钥解密即可，深入了解之后才发现并不是这么简单

下面是使用wireshark抓取的TLS握手阶段的client hello包中所支持的cipher suite：

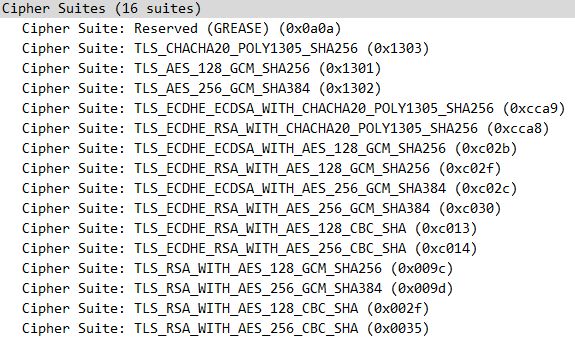
1605469580769

可以看到ECDHE是最多的协商方式，即椭圆曲线DH算法，E代表Ephemeral （短暂的），表示密钥在每次会话结束后就会销毁（保证前向保密性）

可以看到几乎一半的cipher suite都使用了DH算法进行密钥的交换，下面我们来了解一下到底什么是DH算法

DH算法

DH的主要作用是安全地产生一个共享secret，然后使用这个共享secret派生出两个密钥（对称加密）用于后续的消息加密和完整性验证

当今流行的安全协议大多都实现了自己的DH算法，如TLS、SSh、IPsec、PGP等

首先我们用颜色来对DH算法的大致流程进行解释：

img

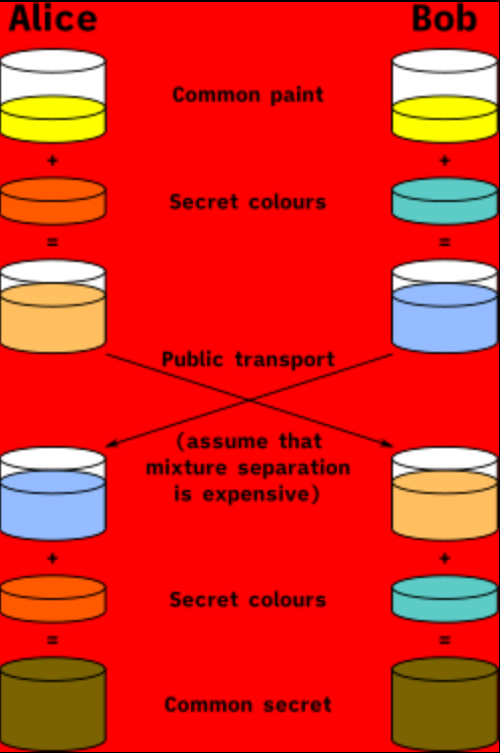
整个过程可以描述为：

  • 双方以一个约定的颜色作为初始颜色
  • 双方各自随机挑选一个颜色，与初始颜色进行混合
  • 双方交换各自混合过后的颜色
  • 双方使用前面的随机颜色与交换过来的颜色进行混合
  • 双方得到最终的共享secret

从上面的过程来看，中间人可以获得初始颜色以及交换的混合后的颜色，通过爆破的方式可以猜解出用于混合的那个随机颜色，最终获得共享secret，当然颜色的爆破可能会比较简单，但是如果是数学计算，就会花费很长的时间和计算资源来进行爆破，而对于DH算法而言，这个时间长（取决于初始数字的长度）到无法接受，因此算法是安全的

可以看到在整个过程中共享secret是从未被传输过的，这就保证了我们可以在不安全的通信信道中安全地进行密钥的交换

下面我们用数学的方式来演示一下整个过程：

  • 首先，Alice和Bob会协商出来一个数字p（这个就是初始数字）和数字g这个数字相对较小（太大的话计算会比较复杂），我们这里假设p为17，g为4

  • Alice随机生成一个数字a，假设为3

  • Bob随机生成一个数字b，假设为6
  • 然后Alice进行运算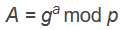：1605174230765，计算出A的值为13
  • Bob进行同样的运算，计算出B的值为16
  • 双方交换AB值
  • 然后各自用交换得到的值替换掉g，进行同样的运算，计算出最后的共享值s，值为16

这里B和s的值相等只是一个巧合，因为我们挑选的数字太小了，实际应用中是不会出现这种情况的

其实就是下面这个等式（注意下面的公式中ab其实不是同一行的，而是指数形式，即g的a次方的b次方）：

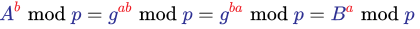
image-20201114094756381

上述过程中的p、g、A、B都是明文传输的， DH算法的安全性基于一个数学上的事实：在仅知道g、ga(A)、gb(B)的值的情况下，无法计算出a和b的值

上面讲解的仅仅涉及到两个人，事实上DH算法支持多方同时进行共享key的创建

在实际应用中，DH不会单独使用，因为它本身不提供认证，无法避免中间人攻击，如果有一个中间人位于Alice和Bob中间，那么最后Alice、Bob和中间人都会得到共享秘钥，从而导致安全信道建立失败，一般的实现都会包括一个电子证书以及公钥加密算法进行签名，比如RSA，我们在上面看到的client hello包中的cipher suite中的RSA以及ECDSA都是用于签名的公钥加密算法

DH算法和RSA的关系

相信不少人都存在这样的疑问：既然RSA同样可以达到让完全陌生的双方进行安全通信（进行秘钥交换），而且还能提供身份认证，那为什么还要再使用DH算法进行秘钥交换呢

这个有几方面：

  • DH算法不同于RSA，在对称秘钥交换方面速度要更快一些
  • 在秘钥交换过程中，由于DH不会传输秘钥，且每次的secret key（这里指的是DH算法计算过程中的随机secret，不是最终的共享secret）都是随机生成的，并会在本次会话完成之后清除交换秘钥过程中产生的所有key，因此是前向安全的（即使本次会话中的long-term key（共享secret）被破解出来，也不会影响到之前会话的安全性），但是RSA就不一样了，如果使用RSA进行秘钥交换，那就需要使用服务器的私钥解密使用服务器公钥加密的共享secret，这样一旦服务器的私钥被破解出来，所有会话的共享secret都会被解密出来（因为公钥并不会经常更换），从而无法保证前向安全

因此RSA算法在秘钥交换过程中起到的作用主要是验证通信双方的身份，服务器向客户端提供自己的证书，客户端使用CA的公钥验证证书的合法性，然后根据证书中提供的服务器相关信息与当前正在进行通信的服务器进行比对以确认服务器身份

TLS中的Pre-Master Secrets和Master Secrets

首先我们来介绍一下MAC算法

何为MAC

这里的MAC是密码学中的名词而不是指网卡，MAC全称Message Authentication Code，翻译过来就是消息认证码

MAC是一种对称加密算法，用于提供消息认证，进行认证的前提条件是收件人和发件人共享一个密钥K

在TLS中MAC被用来进行消息完整性的验证，这个K会由master secrets派生出来

实质上MAC就是一个被加密的校验值，你可以理解为它是用于加密文件的hash值的

MAC

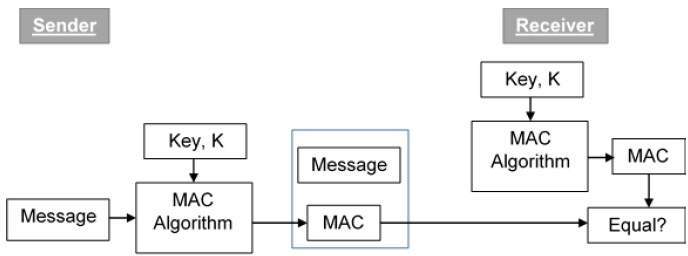
可以看到在发送前发件人先将共享密钥K和要发送的消息消息传给MAC算法，计算出一个MAC值，然后和原始消息（未加密，这里仅作说明只用，实际中传输的消息是被加密的）一起发送给收件人，收件人向MAC算法提供共享密钥K和发送过来的消息，计算出MAC值，如果和发送过来的MAC值相等，则证明消息没有被篡改，同时确认消息来源是可信的

MAC具有以下两个局限性

  • 不提供安全的共享密钥传输渠道
  • 不具备签名功能，因为收发双发均可以计算出相同的MAC，因此收件人可以伪造发件人不曾发送过的消息

不过这两个问题都可以通过公钥加密算法来解决，前者可以使用DH解决，后者可以使用RSA算法进行签名

PRF（伪随机数函数）

在我们加密或者MAC任何东西的时候，我们都绕不过密钥交换的问题

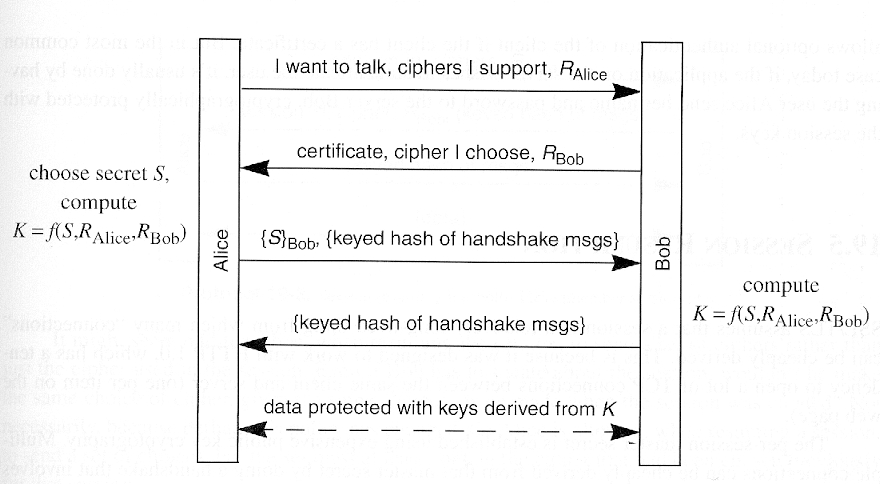
Simplified SSLv3/TLS

pre-master key，也就是图中的S，指的是双方最后协商出来的共享key

协商的方式与client和server在握手阶段选择的cipher suite有关，大部分情况下是DH，不过也有使用rsa的

根据选择的cipher suite，{S}可能是使用服务端证书的公钥（比较少见）进行加密的，也可能是通过DH协商出来的密钥进行加密的

为了保证最后用于加密通信的密钥足够“随机”，我们还需要将pre-master key、client.random和server.random作为参数传到一个函数（prf）中继续进行计算

pre-master key的长度取决于采用的DH算法（DH算法有多种版本）和向算法传递的参数

最终计算出来的master key一般是一个定长的值（也跟选择的cipher suite有关）

RFC中的计算方式：

master_secret = PRF(pre_master_secret, "master secret",
                    ClientHello.random + ServerHello.random)
                    [0..47];

其中两个random是在client hello和server hello消息中发送的，PRF代表伪随机函数

最终生成的master key长度总是48字节，从master key中可以派生出成四个key：

  • client_write_MAC_key
  • server_write_MAC_key
  • client_write_key
  • server_write_key

四个key，分为两类，一个是MAC key，用于验证消息的完整性和来源的可靠性，另一个write key是用于加密消息的对称加密的密钥，虽然是4个key，其实client和server的key是一样的

在handshake阶选择的cipher suite（对称加密算法）决定了这些key的长度，不过其中有一个例外，就是AEAD算法（其实该算法已经是主流的解决方案），它不需要MAC key和write key，而是需要write_IV，AEAD算法的特点就是将加密和认证集成到了一起

常见的 AEAD 算法如下：

  • AES-128-GCM
  • AES-192-GCM
  • AES-256-GCM
  • ChaCha20-IETF-Poly1305
  • XChaCha20-IETF-Poly1305

根据RFC的描述，上面提到的4个key采用下面的方式生成，根据采用的算法，key block产生的数量也会有所不同

key_block = PRF(SecurityParameters.master_secret,
                "key expansion",
                SecurityParameters.server_random +
                SecurityParameters.client_random);

现在我们来解释一下PRF函数

RFC中关于TLS v1.1中PRF函数的说明，和TLS v1.2有所不同，PRF的定义：

PRF(secret, label, seed) = P_<hash>(secret, label + seed)

采用go语言实现的PRF函数：https://golang.org/src/crypto/tls/prf.go#L145

P_hash(secret, seed) = HMAC_hash(secret, A(1) + seed) +
                       HMAC_hash(secret, A(2) + seed) +
                       HMAC_hash(secret, A(3) + seed) + ...

其中函数A的定义为：

A(0) = seed
A(i) = HMAC_hash(secret, A(i-1))

当计算的结果满足我们需要的master key长度时，迭代计算就会停止，结果也就出来了，计算key_block同理

下面是对go语言实现的prf的代码注释：

//按照RFC中的说明，将pre-master key分成两部分
func splitPreMasterSecret(secret []byte) (s1, s2 []byte) {
    s1 = secret[0 : (len(secret)+1)/2]
    s2 = secret[len(secret)/2:]
    return
}

//实现RFC中提到的P_hash函数
func pHash(result, secret, seed []byte, hash func() hash.Hash) {
    //此处的hmac包所实现的函数是前面提到的MAC算法，对消息的hash进行加密，以进行消息发送者身份的验证
    //首先创建出一个hmac对象，它接收连个参数，前者是hash算法，后者是加密使用的key
    h := hmac.New(hash, secret)
    //seed即为要加密的消息
    h.Write(seed)
    //a就是最后求得的MAC值
    a := h.Sum(nil)


    j := 0
    //就像我们在文章前面提到的，hmac会进行迭代运算直到满足预定的长度
    //这里的result是填充了指定个数的0的数组
    //等到长度满足要求之后master-key的计算也就完成了
    for j < len(result) {
        //重置h，清空之前的消息
        h.Reset()
        //写入前面计算出来的seed的MAC值
        h.Write(a)
        //根据文章中提到的，每次进行MAC的计算都会加上seed，因此在写入a之后还要再写入seed
        //前面只写了seed是因为A(0)=seed
        h.Write(seed)
        //代码读到这里我们可以看到go语言的这段代码完全是按照RFC的说明进行实现的
        b := h.Sum(nil)
        //将求得的结果写入result
        copy(result[j:], b)
        //记录一下本次写入的长度
        j += len(b)

        //对于第一次循环，i=1，A(1) = HMAC_hash(secret, A(0)) = HMAC_hash(secret, seed) = a
        //下面的计算是为第二次循环做准备，也就是要求A(2)的值
        //这里求得的a其实就是A(2) = HMAC_hash(secret, A(2-1)) = HMAC_hash(secret, a)
        h.Reset()
        h.Write(a)
        a = h.Sum(nil)
    }
}

//go语言实现的prf函数（这个是TLS 1.0版本），接收四个参数，其中第一个result是传出参数，用于保存计算得到的master-key
//第二个参数secret是之前计算出来的pre-master key
//seed字节数组就是client.random + server.random
func prf10(result, secret, label, seed []byte) {
    //sha1和md5都是摘要算法（hash算法）
    hashSHA1 := sha1.New
    hashMD5 := md5.New

    //创建出一个长度为label和seed长度之和的数组，然后将label和seed填充进去
    labelAndSeed := make([]byte, len(label)+len(seed))
    copy(labelAndSeed, label)
    copy(labelAndSeed[len(label):], seed)

    //将pre-master key分成s1和s2两部分
    s1, s2 := splitPreMasterSecret(secret)
    //将分开之后的pre-master key分别进行pHash运算，将求得的两个值进行异或运算
    pHash(result, s1, labelAndSeed, hashMD5)
    result2 := make([]byte, len(result))
    pHash(result2, s2, labelAndSeed, hashSHA1)

    for i, b := range result2 {
        result[i] ^= b
    }
}

//这是TLS 1.2版本的prf实现代码，可以看到和我们文章中描述的是一致的，直接使用pre-master key进行计算，没有进行分割
func prf12(hashFunc func() hash.Hash) func(result, secret, label, seed []byte) {
    return func(result, secret, label, seed []byte) {
        labelAndSeed := make([]byte, len(label)+len(seed))
        copy(labelAndSeed, label)
        copy(labelAndSeed[len(label):], seed)

        pHash(result, secret, labelAndSeed, hashFunc)
    }
}

后记

文章中还有很多不够完善的地方（比如write_IV密钥的计算方法以及对https通信进行抓包分析），后面如果有空会再继续进行更新 ：）